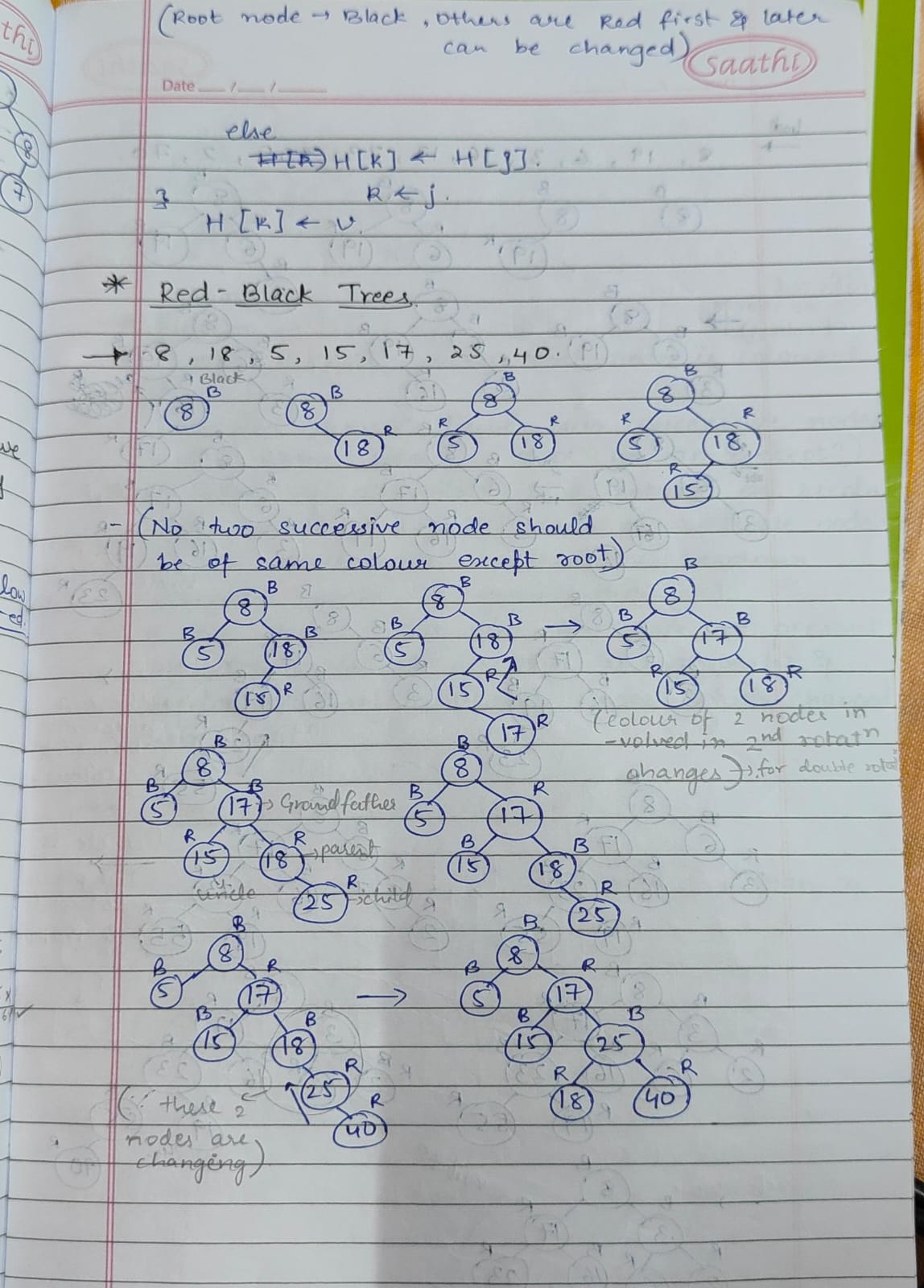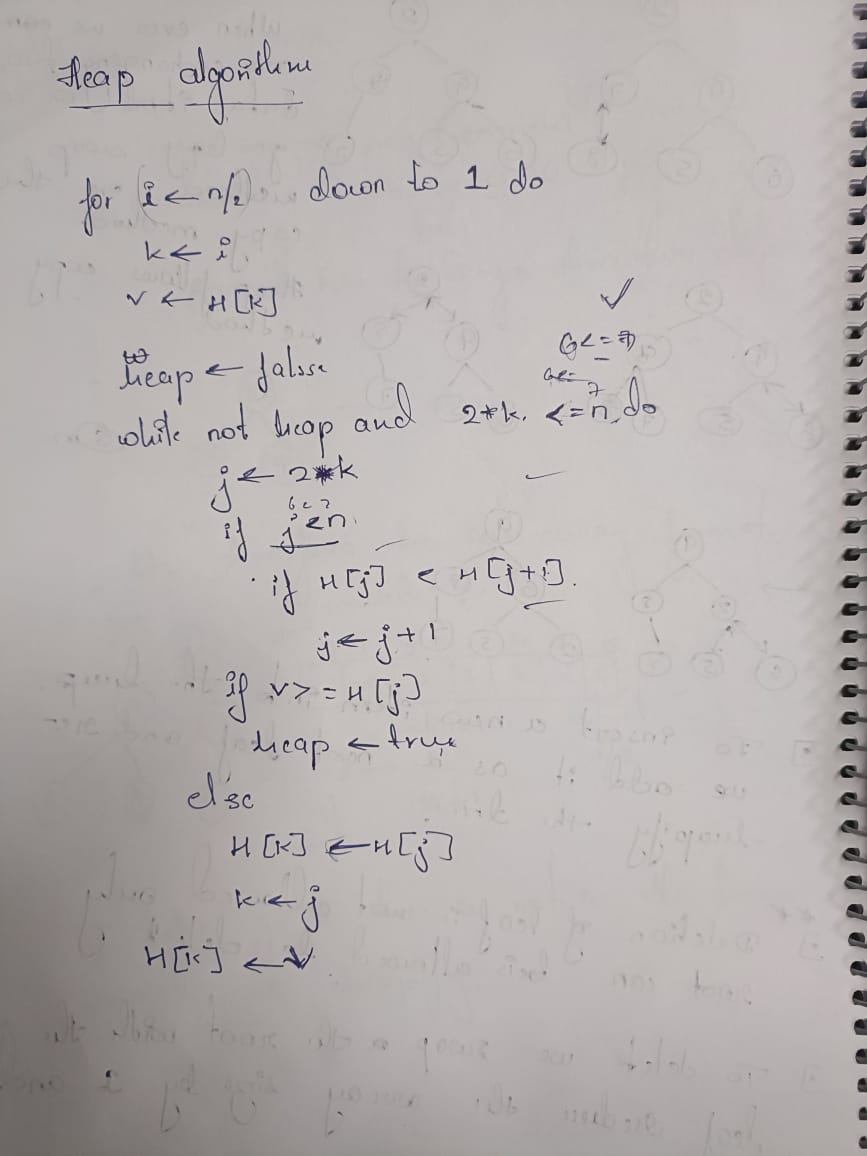Course Reflection

Home Course Reflection
course learnings

LEARNINGS FROM THE COURSE

-> Hierarchical data structures like trees organize information in parent-child relationships. BST enables fast searches, but balancing is crucial, addressed by AVL or Red-Black trees. Heaps manage priority tasks efficiently, while Tries excel in prefix searches like auto-complete. Each tree optimizes specific operations, making them vital for various applications.
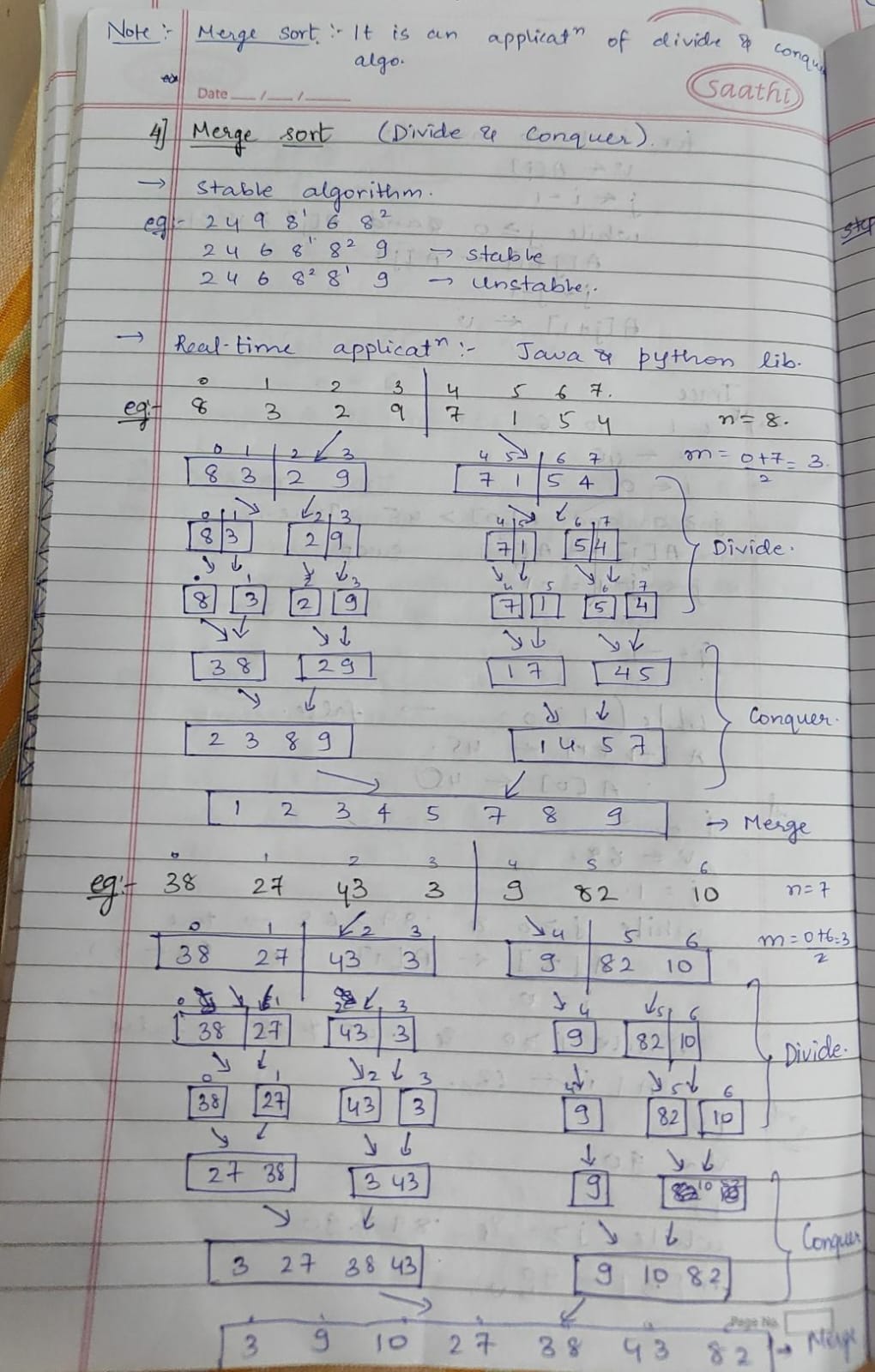
-> Array query algorithms solve problems like range sums or maximum values efficiently. Segment Trees and Fenwick Trees allow logarithmic time operations, handling even large datasets. These algorithms are crucial in data analytics, competitive programming, and real-time systems requiring quick computations.
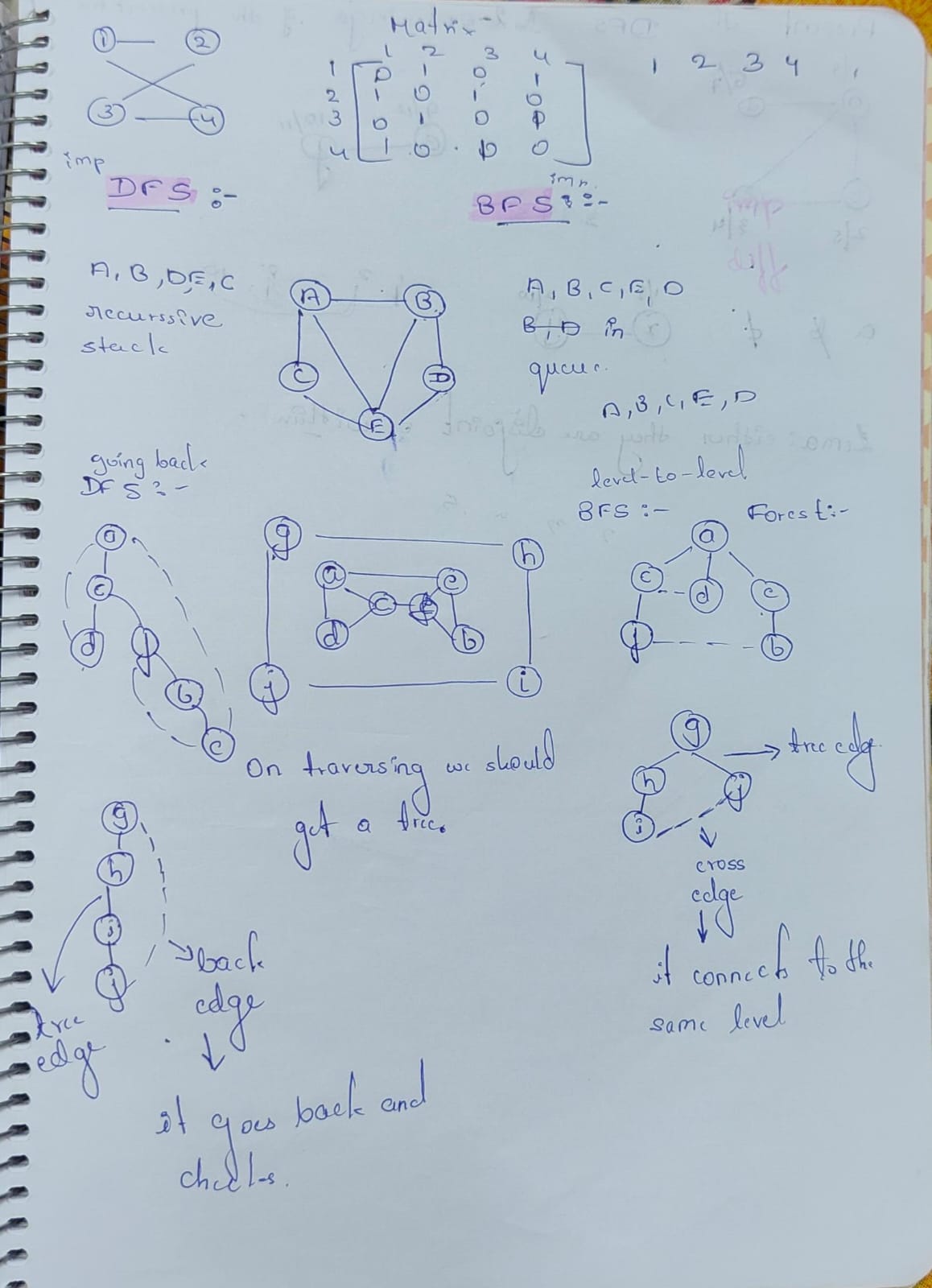
-> Trees are hierarchical and cycle-free, used in structured data like file systems. Graphs are flexible with complex connections, ideal for networks and paths. Tree traversals (Inorder, Preorder) suit hierarchy processing, while graph traversals (BFS, DFS) explore connectivity and shortest paths.
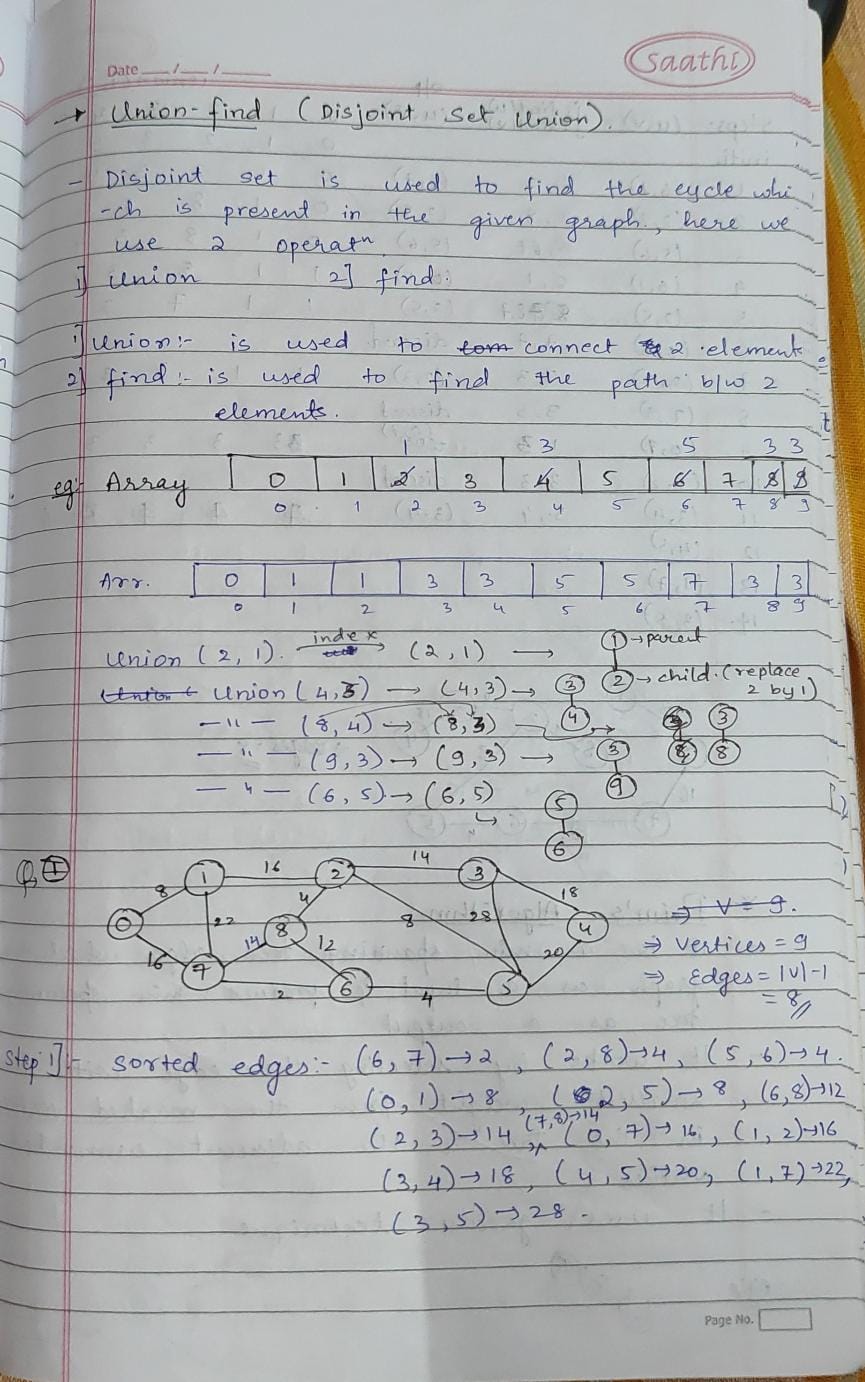
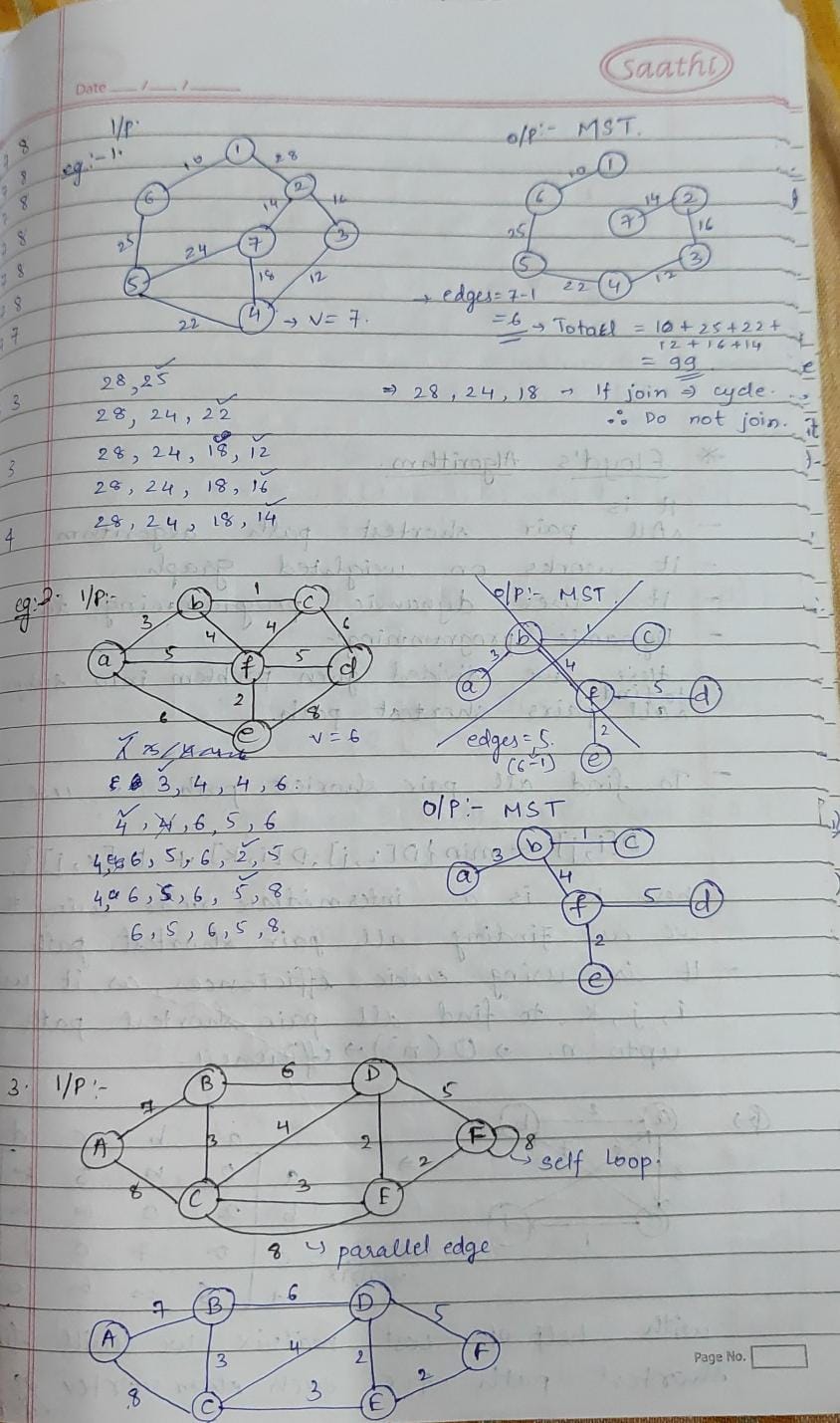
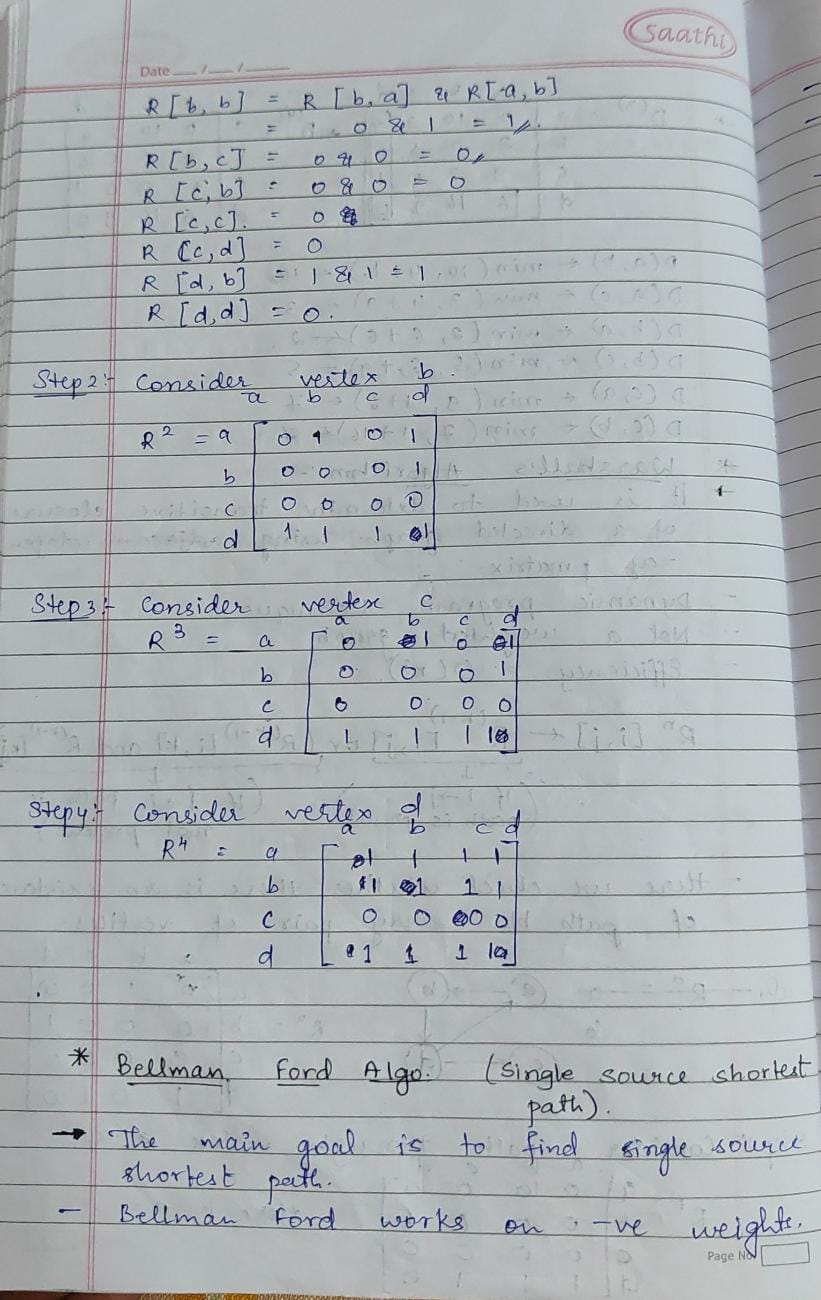
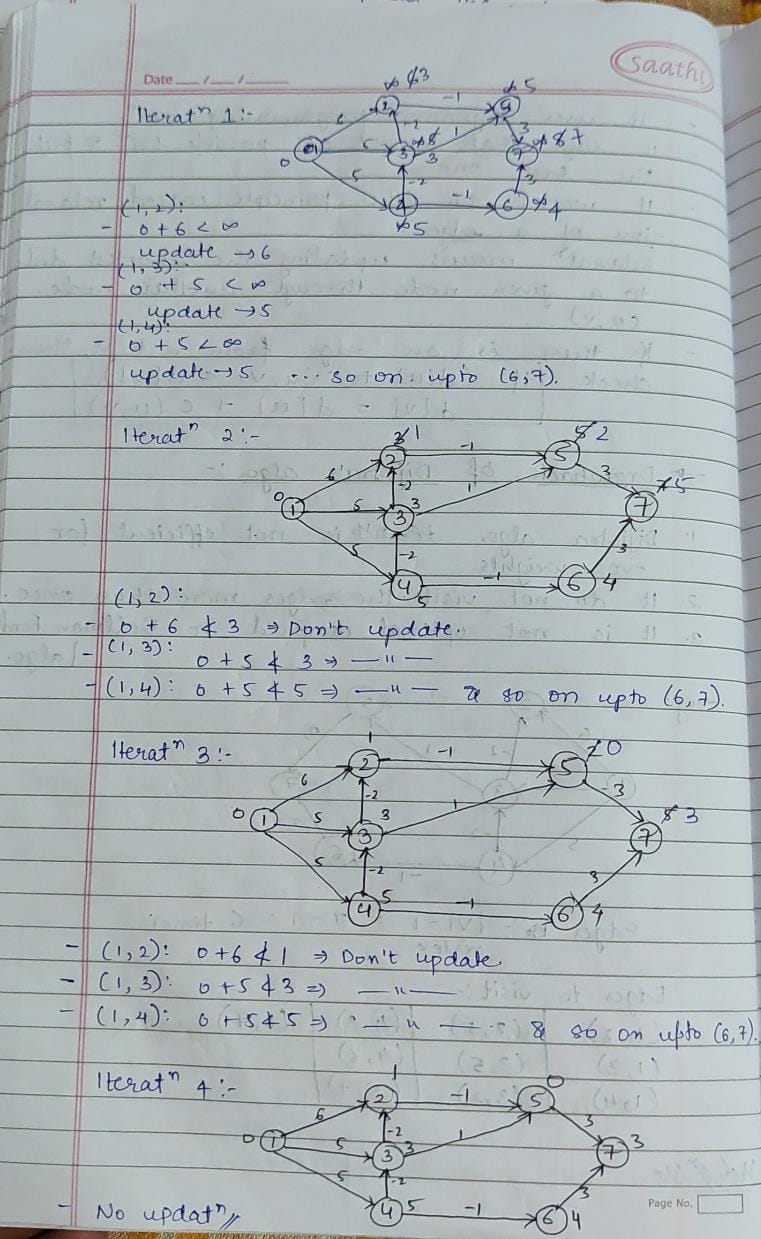
-> Spanning tree algorithms like Kruskal’s minimize costs in network design. Shortest path algorithms like Dijkstra’s are essential for navigation apps and logistics. These algorithms optimize connectivity and route planning in real-world networks, enhancing efficiency.
Image 1
Image 2
Image 3
Image 4
Image 5
Image 6
Image 7
Image 8
Image 9
Nature's Computational Patterns

Understanding Iteration, Recursion, and Backtracking

Iteration: A process where a set of instructions is repeated in a loop until a specific condition is met. It is widely used in computations like traversing arrays or solving mathematical problems.

Recursion: A method of solving problems where a function calls itself as a subroutine. It simplifies solving complex problems by breaking them into smaller, identical tasks.

Backtracking: A problem-solving technique that involves exploring all possible paths to find solutions, retracting steps when a path leads to a dead end. It is often used in puzzles, pathfinding, and constraint satisfaction problems.

Iteration
Iteration

Repeated patterns, like the spirals in seashells, exemplify the power of iterative processes.

Recursion
Recursion

Fractal patterns in snowflakes demonstrate recursive structures in nature.

Backtracking
Backtracking

Ants searching for food mimic backtracking by exploring and retracting paths.

Principles

Principles of Design and Analysis of Algorithms

  • Decomposition: Breaking a complex problem into smaller, manageable sub-problems to simplify analysis and solution development.
  • Pattern Recognition: Identifying recurring structures or behaviors in data or algorithms to leverage reusable solutions.
  • Abstraction: Focusing on essential details and ignoring unnecessary complexities to simplify the problem-solving process.
  • Lazy Propagation/Evaluation: Delaying computation until absolutely necessary, commonly used in segment trees and other optimization algorithms.
  • Sliding Window: A technique for efficiently solving problems that involve subarrays or substrings, optimizing space and time complexity.
  • Pruning: Eliminating unnecessary computations or paths in a search space to optimize performance, as in branch-and-bound algorithms.
  • Memoization and Pre-computing:
    • Memoization: Storing intermediate results during runtime to avoid redundant computations.
    • Pre-computing: Calculating and storing results beforehand for static data to improve runtime efficiency.
Efficiency Matters

Space Efficiency

Space efficiency refers to the ability of an algorithm or program to use a minimal amount of memory (space) while still achieving the desired results. It measures how effectively a program utilizes memory resources to perform its task, aiming to reduce unnecessary memory consumption. A space-efficient algorithm minimizes the amount of memory required, which is particularly important in environments with limited memory (such as embedded systems) or when processing large datasets.
  • -> Hash Tables
  • -> Lookup Tables
  • -> Database Indexing

Space

And

Time

Trade-off

The time-space trade-off is a concept in computer science that’s about balancing two things: how much memory an algorithm needs and how long it takes to run.
Efficiency Matters

Time Efficiency

Time efficiency refers to the ability of an algorithm or program to complete its task in the least amount of time possible, relative to the size of the input. It measures how quickly an algorithm executes, aiming to minimize the time required to produce the desired result. Time efficiency is important for improving the performance of applications, especially when dealing with large datasets or time-sensitive tasks.
  • -> Memoization in Dynamic Programming
  • -> Sorting with Extra Memory
  • -> Breadth-First Search (BFS) in Graphs

My Notes

DEVELOPED BY
Ananya Hiregoudar

© 2025 DESIGN AND ANALYSIS OF ALGORITHMS. All rights reserved.